《游戏学导论》- 第九、第十讲

这两次课专注讨论“博弈”本身,通过大量的博弈概念解释串了一遍博弈论本身及延申到游戏下的具体示例,总共 10 个定理,我深深的感受到原来日常中所经历了一些事情在博弈论里经过一番抽象和完善后竟被剥离得如此露骨,就彷佛背后有只手在推动我们去做一些事情,做的这些事情又都是被这只大手给操纵的。
10 个定理
老师通过引出博弈论的老祖冯诺依曼自己两个女儿分馅饼的故事引出了博弈论和人工智能雏形,故事是这样的。不管怎么家人怎么分馅饼,两个女儿总是会觉得不公平,冯诺依曼最终选择了一个巧妙地方法,让两个女儿自己分馅饼,如果大女儿切馅饼那么小女儿先挑,如果小女儿切馅饼,那么大女儿先挑。
这种由局中人自行决定选项的办法屡次不是,为了保证绝对的公平两个女儿在分别负责切馅饼的时一定不会让自己吃亏,因为谁切馅饼谁最后选。通过这个问题就瞬间把我们拉入博弈论中。关于游戏和博弈论的关系,博弈是游戏存在的基础,博弈也是一种思维方式,是策划在制定规则时的基本保障,也是玩游戏时能迅速找到解的核心。
由此引出了第一条定理:若系统存在规则或机制的漏洞,必定有用户理该漏洞为自己获取最大利益。
博弈论的前提是要考虑人性逐利的本性,博弈论中的所有利益参与者,全部属于个体绝对理性角色,换句话说就是所有角色以满足自己长远利益最大化为优先策略,若需要以伤害他人为利益最大化的前提条件,参与者就会损人利己。博弈论最早作为运筹学的一个分支,作为经济学的补充存在,而经济行为就是之前的提到的“日常游戏”,且是稍有的可以 save/load 的日常游戏,仔细想想金融领域里的操作行为如炒股、基金买卖等等行为确实是像一个游戏。它是研究当两个或多个决策主体之间存在相互作用,任何一方的决策策略都不能完全独立于其他各方策略时,各方的策略过程以及均衡问题。
这里引出了“纳什均衡”这里非常著名的概念:一个策略集合,其中每个参与人没有动机去单方面改变自己的行动。任何一个人改变策略都会获得更少的利益,这就是纳什均衡。并把第二条定理也总结了出来:如果一种游戏系统的规则以及机制安排要发生效力,该游戏必须能达到纳什均衡,否则这种制度安排就没有效力。
进入到下一个博弈模型“囚徒博弈”,这个模型我们都比较熟悉,它属于“完全信息静态博弈”,指的是博弈各参与方同时行动,且对博弈相关信息完全了解,常用于设计即时类游戏,老师拿了以下四个博弈模型做了解释,没想到的是老师居然把素质教育和应试教育也拿来做了模型,这么一对比给出了惊人的结论,在中国搞素质教育是根本不可能的,佩服老师直面问题的魄力。

引出了定理3:在游戏规则的制定中,利用纳什均衡能保证系统和谐稳定,如果鼓励玩家合作,则需要避免囚徒博弈,并修改规则使之倾向于猎鹿博弈。反之,游戏不鼓励合作则尽可能设置囚徒博弈。
接下来的定理4,老师通过猎鹿博弈和智猪博弈来说明。
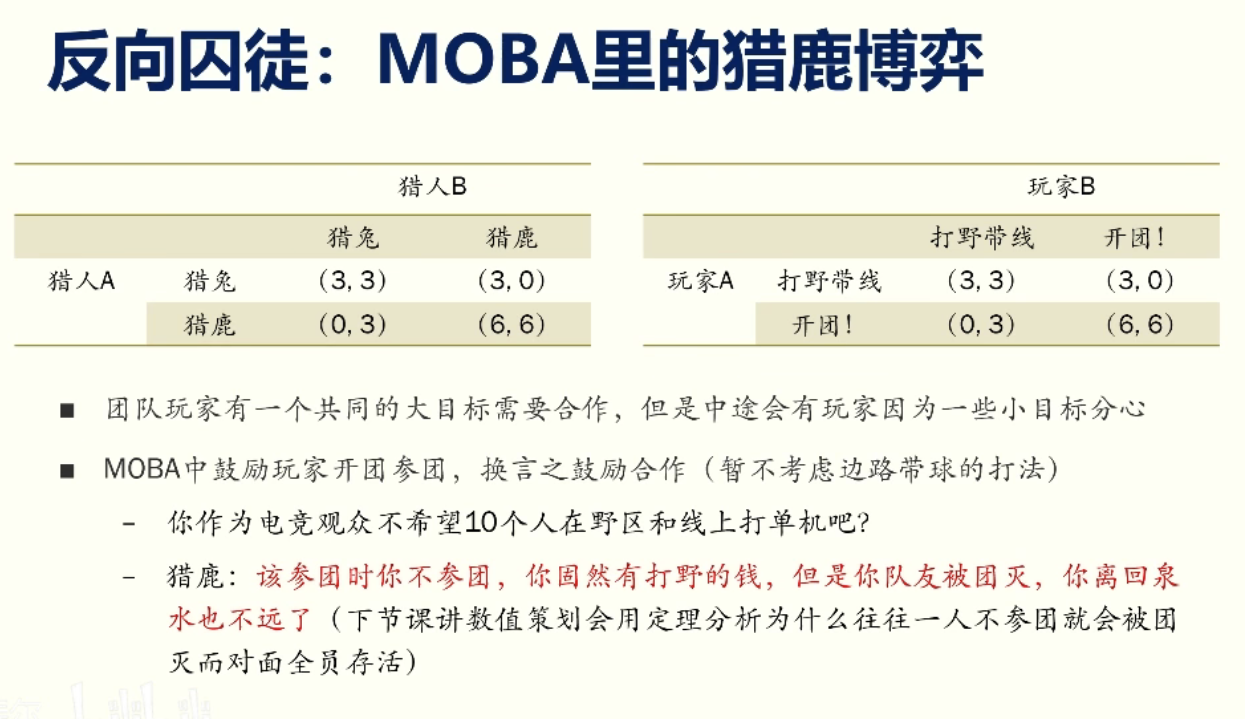

在智猪博弈中,老师举了抱大腿的例子,学霸和学渣组成一对,如果学渣不想努力,学霸想努力,学霸的收益 100 分,而学渣因为抱大腿拿了 70 分;如果学渣努力,学霸也努力,学霸 100 分,学渣因为自己努力了可以拿到 80 分;但如果二者均不想努力,二者都是 0 分,身为学霸一定会让自己尽可能的拿到 100 分,而学渣不管努不努力都可以拿到收益,这样学渣一定不会努力,而学霸一定会努力。到头来这二者就变成了智猪博弈模型里的大猪一定每次都会按开关。
仔细想想这个智猪博弈模型用在现实生活中真的很有趣,如果真的出现了这个问题那有没有解决的办法呢?在暗黑中老司机带刷图会对低等级玩家获得的经验减半,这点其实在之前玩的很多游戏中都遇到过,在《征服》中也是如此,要不然高等级怪物带给低等级玩家的经验值过于恐怖。还有一些如可置信威胁、日式霸凌、任务量可视化甚至减少团队成员数量并明确分工这种具体的措施等等。
而定理 4 为:在团队游戏规则的制定中,如果较弱的用户能够通过智猪博弈绑架其他用户获得正收益,则必有玩家永远选择利益绑架。智猪博弈是团队规则与合作的天敌,团队个体数量越多,智猪的隐蔽性越强。
定理 5 比较容易理解:如果设定的游戏机制有明显的僵局,那么调整博弈收益使其符合性别博弈,可以有效地挑动玩家主动参与,且在即时性游戏里会擦出极其美妙的火花。

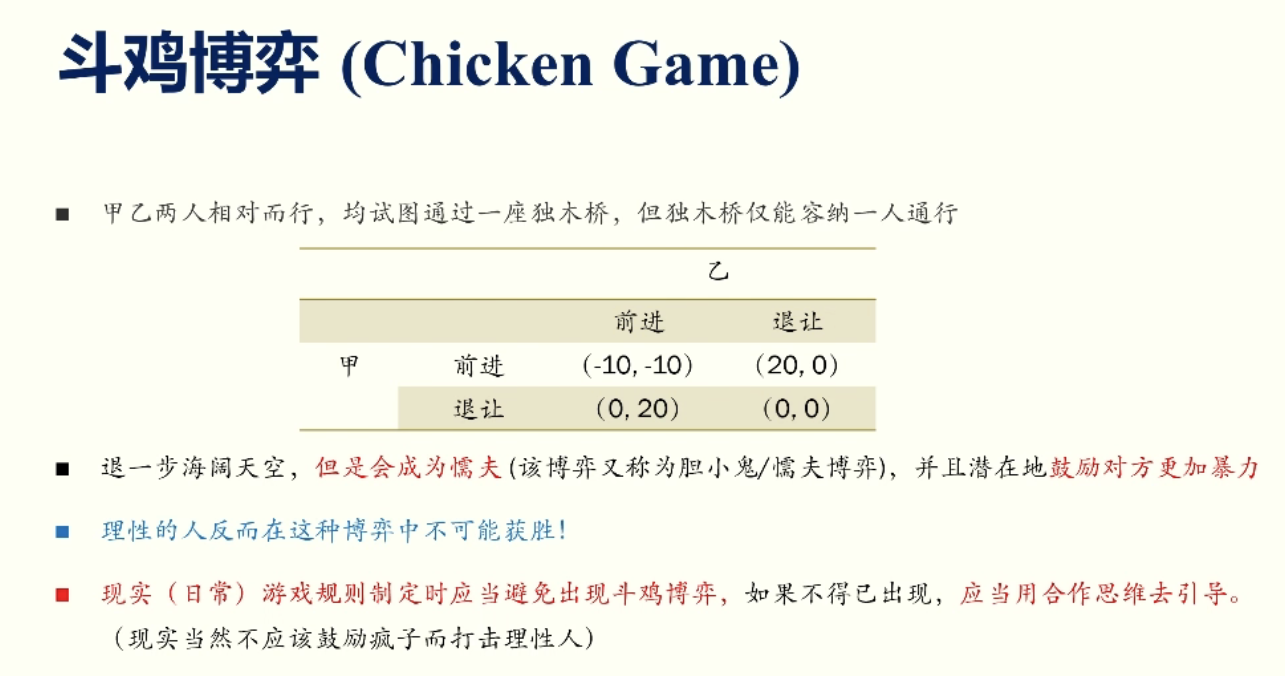
定理 6 :斗鸡博弈中理性玩家无法获得最后的胜利,斗鸡博弈要避免在团队规则中出现,但鼓励在对抗规则中涉及。消除斗鸡博弈与志愿者困境,可以给理性退让者对应的收益。

定理 7:纳什均衡存在性定理:如果博弈参与者为有限个,而且每个博弈参与者所能选择的策略也是有限个,则该博弈至少存在一个纳什均衡(纯策略均衡或者混合策略均衡)。
到了定理 8,引入了“静态博弈”和“动态博弈”,在智猪模型中给到的破局方法都是动态博弈的具体方法,而采用静态博弈是无法进行破局的。静态博弈指的是:参与者同时选择,或虽非同时选择,但是在逻辑时间上是同时的;动态博弈指的是:参与者的行动有先后顺序,且后行动者能够观察到先行动者的行动。这里放一张老师的幻灯片,看看通过动态博弈的博弈树是如何破解学霸学渣智猪模型的:
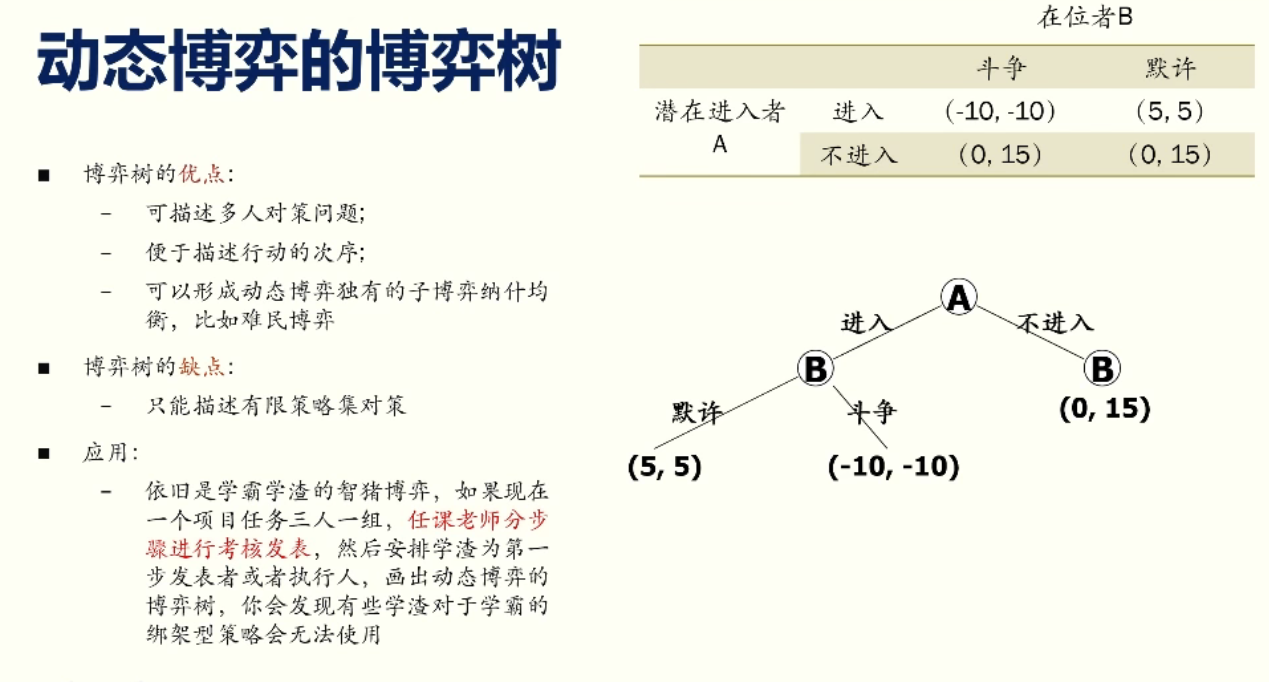
通过这两点引出了定理 8:静态博弈与动态博弈对于策略威胁的纳什均衡可能存在变化,信息透明的前提条件下,动态博弈可以有效地精练同等条件下静态博弈产生的混合战略纳什均衡。
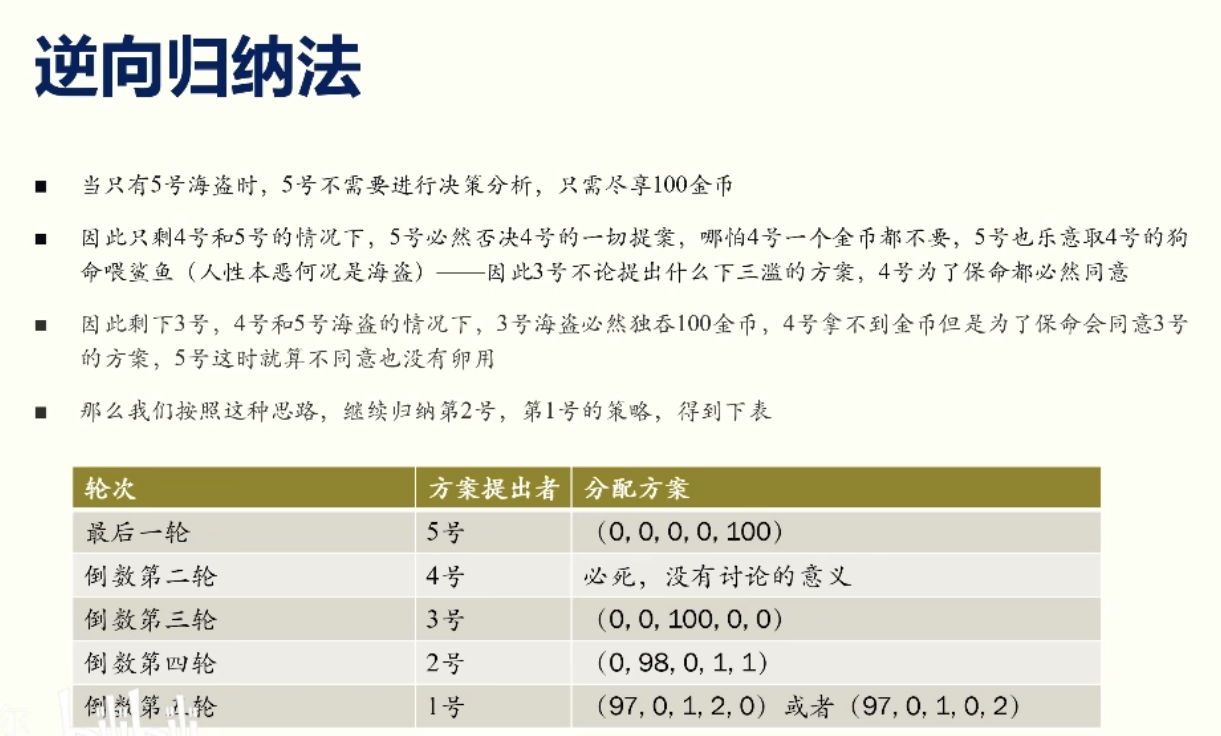
老师接着通过“海盗分金币”的方法引出了“逆向归纳法”,海盗分金币的问题指的是现在有 5 个海盗要分 100 个金币,每个海盗都提出一个金币分配方案,当有 3 个海盗赞成该方案就通过,反之把该海盗丢到海里喂鲨鱼。刚开始我看到题目时还在使用正常思维从上到下的思考,没想到通过引入逆向归纳法后不但解决了这个问题还能保证了海盗 1 的利益最大化。
老师还给到了“重复博弈”这个概念,我个人感觉这有点像“动态规划”概念有点相似,动态规划是把目标问题拆为几个子问题,通过求解这些子问题来拿到最终问题的解,而重复博弈指的是相同的结构的博弈重复多次,所有博弈中的角色都可以观测到每次博弈的结果,并对当下做出判断。说到为什么要研究重复博弈的话,人们之间的长期关系与短期关系之间有重要的性质差别,人们在对待与其有长期关系的人与对待那些以后不再交往的人可能会有非常不同的行为。重复博弈中,局中人可能会为了长远利益,而牺牲眼前利益。
课程进展到老师说了个有趣的思考,博弈论的研究者容易形成法家思想,也即制定规则时不要信任玩家。定理 9:如果阶段博弈 G 有唯一的纳什均衡,那么对任意有限次重复博弈 G(T) 有唯一的子博弈精炼纳什均衡结果:G 的纳什均衡重复 T 次。除非引入外力因子破坏纳什均衡。
最后一个定理 10:如果博弈重复无穷次,且每个人有足够的耐心,任何短期的机会主义行为的所得都是微不足道的。参与人有积极性为自己建立一个乐于合作的声誉,同时也有积极性惩罚对方的机会主义行为,所以制定合理的游戏规则还可以从长远利益入手。定理 10 用字节的话来说就是“延迟满足感”,看来天下之士对核心价值观都有着一定的趋同性啊!
思考
以上这 10 个定理及其背后关联的故事案例都给到了我极大的印象,很多东西之前完全没有思考过,就算在课上跟着老师一块想也在拿着现有的思维去套,很多东西套着套着就走不出来了,不管怎么算都进到了仿佛被设计好的圈套中。